TECH TOPICS: Speed
Article and illustrations by John Henderson. Photos by Judy Bonanno
How fast do our models go, really? They always look fast—well, at least I tell myself that mine look fast to me— but what answer do we get if we try to quantify their speed?
The standard equation for “hull speed” that is often quoted in magazine articles is:
Equation 1
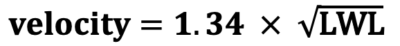
where velocity is given in knots, the Load Waterline Length (LWL) is in feet, and “hull speed” is understood to be a sort of maximum practical speed.
Fig. 1. Drawings of the bow and stern waves
generated by a displacement boat’s motion.
Under what conditions is this equation true? How accurate is it? Does it apply to boats of all sizes? Why are speed and length related this way?
The first qualifier is that Equation 1 applies to displacement boats. That is, boats that cannot plane or at least are not planing when we apply this equation. “Displacement” means that the boats are supported solely by their inherent buoyancy. They have not risen up on their bow wave as planing boats do. Virtually all of our model sailboats operate in displacement mode.
Boats are slowed by resistance, which comes from both “skin friction” and the energy losses caused by making waves. Skin friction dominates at low speeds (light air) and is not the big contributor to the practical upper speed limit described by Equation 1. The conditions that concern this article —losses due to wave making—are found with higher winds and higher boat speeds.
The practical speed limit implied by Equation 1 is caused by wave-making. We have all seen the bow and stern waves and the wakes that our models make when they are going fast. Making these waves requires energy, and this energy loss limits boat speed. The waves tend to get bigger as our boats go faster, with more and more energy loss until our sails just can’t extract enough power from the wind to go any faster.
Fig. 2. Rainbow with a wave train nearly equal to the LWL.
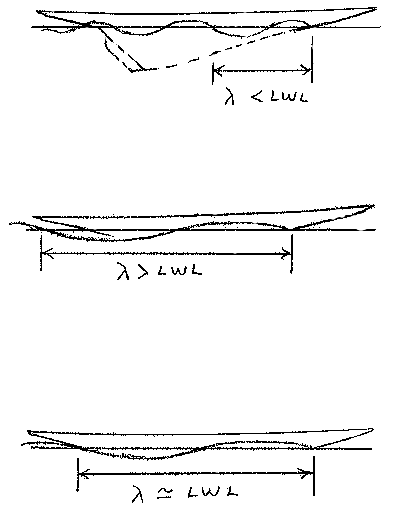
Fig. 1 contains three drawings of the bow and stern waves generated by a boat’s motion, and it supports the conclusion that these wave trains change with boat speed.
The wavelength of the waves generated by the boat’s motion is designated by the Greek letter lambda, λ. Note that, at low speeds (top drawing), the wave train has several waves along the LWL, indicated on the drawing as “λ < LWL.” The number of waves diminishes (and the waves become longer) as speed increases. When λ exceeds the waterline length (middle drawing), the boat’s stern will drop down into the trough (note the bow-up attitude), and the boat appears to be trying to climb up onto its bow wave. A displacement boat is not able to do this with practical power levels. The third drawing shows the wave train when λ and the LWL are approximately equal. This is the speed predicted by Equation 1, which will likely be the practical upper limit to speed in a displacement boat of “usual” proportions (like our models).
Fig. 3. Rainbow’s wake and following wave train.
Before anyone dismisses this discussion as idealized drawings in a textbook, let’s look at some photos of model boats underway. Figures 2 and 3 are photos of the author’s 6-ft model of the J-boat Rainbow, taken by Judy Bonanno at the 2021 Vintage Nationals. Fig. 2 clearly shows the bow wave at the forward end of the waterline and the stern wave aft; it is apparent that one single wavelength is almost as long as the LWL. The boat is traveling at a speed approaching “hull speed.” Fig. 3 shows the wake, and it clearly reveals about three wavelengths of the resulting “transverse” wave train following the boat. This matches the textbook exactly.
Equation 1, however, teaches us something more quantitative. The speed limit is proportional to the square root of the waterline length. We all accept the idea that big boats go faster than little boats, but why does the speed depend on a square root, and where did the proportionality factor of 1.34 come from?
To make some sense of this square root relationship and the peculiar factor of 1.34, I will refer to C.A. Marchaj’s book Sailing Theory and Practice. After more physics than would be polite in a family magazine like this one, he presents an equation that relates the speed of propagation of a surface wave in water (v) to its wavelength (λ):
λ (ft) [/column] = 2πv2/g,
where “g” (the acceleration due to gravity) = 32.17 ft/s2
= 0.195v2, when v is in ft/s
= 0.557v2, when v is in knots (nautical miles/hour).
Rearranging the last expression yields
Equation 2
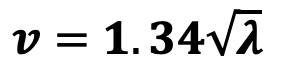
which is Equation 1 if λ is replaced by LWL (in units of feet). This means that when a boat is traveling at a speed where one wavelength of the wave train the boat generates is equal to the waterline length, then that wave – and consequently the boat – is traveling at a speed given by Equation 1. This is a practical speed limit, because the boat is “trapped” in its own wave train; it cannot climb out of this trap without applying more power than our sails can generate.
More bad news: Normal sailing yachts probably will not reach this speed except under unusual circumstances. From what I have read, a speed of 
might be more typical, sometimes even less for beamy and heavy-displacement boats, whose waves, even though the wavelength is given by Equation 1, are bigger. Bigger waves take up more energy and make a trough that is harder to overcome. Dedicated racing boats, even displacement boats, might go a little faster than Equation 1. A factor of 1.45 is claimed for something like a J-Class yacht.
For a 4-ft long (LWL) model, the hull speed, using the 1.34 factor, is (only) about 2.7 knots. Sorry. But it still looks fast.
All of this applies to boats of “normal” shape, which I think includes virtually all of our “vintage” boats. Other shapes, which might make smaller waves, could exceed the speed predicted by the equations above because the smaller waves they generate extract less energy from the propulsion forces. Examples of such shapes would be racing kayaks, rowing shells, catamarans, and other multihulls. It is not that the speed of wave propagation changes, but rather that the light and narrow hulls may be able to “climb” their much smaller bow waves. Planing hulls (when actually planing), including sailing dinghies like the Laser, also exceed displacement hull speeds.